UTILIZANDO CURIOSIDADES E JOGOS MATEMÁTICOS EM SALA DE AULA

Curiosidades e Jogos matemáticos como recurso didático

 

Ensinar matemática é desenvolver o raciocínio lógico, estimular o pensamento independente, a criatividade e a capacidade de resolver problemas. Nós, como educadores matemáticos, devemos procurar alternativas para aumentar a motivação para a aprendizagem, desenvolver a autoconfiança, a organização, concentração, atenção, raciocínio lógico-dedutivo e o senso cooperativo, desenvolvendo a socialização e aumentando as interações do indivíduo com outras pessoas.

Os jogos, se convenientemente planejados, são um recurso pedagógico eficaz para a construção do conhecimento matemático. Referimo-nos àqueles que implicam conhecimentos matemáticos.

Vygotsky afirmava que através do brinquedo a criança aprende a agir numa esfera cognitivista, sendo livre para determinar suas próprias ações. Segundo ele, o brinquedo estimula a curiosidade e a autoconfiança, proporcionando desenvolvimento da linguagem, do pensamento, da concentração e da atenção.

O uso de jogos e curiosidades no ensino da Matemática tem o objetivo de fazer com que os adolescentes gostem de aprender essa disciplina, mudando a rotina da classe e despertando o interesse do aluno envolvido. A aprendizagem através de jogos, como dominó, palavras cruzadas, memória e outros permite que o aluno faça da aprendizagem um processo interessante e até divertido. Para isso, eles devem ser utilizados ocasionalmente para sanar as lacunas que se produzem na atividade escolar diária. Neste sentido verificamos que há três aspectos que por si só justificam a incorporação do jogo nas aulas. São estes: o caráter lúdico, o desenvolvimento de técnicas intelectuais e a formação de relações sociais.

Jogar não é estudar nem trabalhar, porque jogando, a aluno aprende, sobretudo, a conhecer e compreender o mundo social que o rodeia.

Os jogos são educativos, sendo assim, requerem um plano de ação que permita a aprendizagem de conceitos matemáticos e culturais de uma maneira geral. Já que os jogos em sala de aula são importantes, devemos ocupar um horário dentro de nosso planejamento, de modo a permitir que o professor possa explorar todo o potencial dos jogos, processos de solução, registros e discussões sobre possíveis caminhos que poderão surgir.

Os jogos podem ser utilizados pra introduzir, amadurecer conteúdos e preparar o aluno para aprofundar os itens já trabalhados. Devem ser escolhidos e preparados com cuidado para levar o estudante a adquirir conceitos matemáticos de importância.

Devemos utilizá-los não como instrumentos recreativos na aprendizagem, mas como facilitadores, colaborando para trabalhar os bloqueios que os alunos apresentam em relação a alguns conteúdos matemáticos.

'' Outro motivo para a introdução de jogos nas aulas de matemática é a possibilidade de  diminuir bloqueios apresentados por muitos de nossos alunos que temem a Matemática e sentem-se incapacitados para aprendê-la. Dentro da situação de jogo, onde é impossível uma atitude passiva e a motivação é grande, notamos que, ao mesmo tempo em que estes alunos falam Matemática, apresentam também um melhor desempenho e atitudes mais positivas frente a seus processos de aprendizagem.''

(Borin,1996,9)

Segundo Malba Tahan, 1968, ''para que os jogos produzam os efeitos desejados é preciso que sejam, de certa forma, dirigidos pelos educadores''. Partindo do princípio que as crianças pensam de maneira diferente dos adultos e de que nosso objetivo não é ensiná-las a jogar, devemos acompanhar a maneira como as crianças jogam, sendo observadores atentos, interferindo para colocar questões interessantes (sem perturbar a dinâmica dos grupos) para, a partir disso, auxiliá-las a construir regras e a pensar de modo que elas entendam.

Moura, 1991, afirma que ''o jogo aproxima-se da Matemática via desenvolvimento de habilidades de resoluções de problemas''.

Devemos escolher jogos que estimulem a resolução de problemas, principalmente quando o conteúdo a ser estudado for abstrato, difícil e desvinculado da prática diária, não nos esquecendo de respeitar as condições de cada comunidade e o querer de cada aluno. Essas atividades não devem ser muito fáceis nem muito difíceis e ser testadas antes de sua aplicação, a fim de enriquecer as experiências através de propostas de novas atividades, propiciando mais de uma situação.

Os jogos trabalhados em sala de aula devem ter regras, esses são classificados em três tipos:

• jogos estratégicos, onde são trabalhadas as habilidades que compõem o raciocínio lógico. Com eles, os alunos lêem as regras e buscam caminhos para atingirem o objetivo final, utilizando estratégias para isso. O fator sorte não interfere no resultado;
     
• jogos de treinamento, os quais são utilizados quando o professor percebe que alguns alunos precisam de reforço num determinado conteúdo e quer substituir as cansativas listas de exercícios. Neles, quase sempre o fator sorte exerce um papel preponderante e interfere nos resultados finais, o que pode frustrar as idéias anteriormente colocadas;
     
• jogos geométricos, que têm como objetivo desenvolver a habilidade de observação e o pensamento lógico. Com eles conseguimos trabalhar figuras geométricas, semelhança de figuras, ângulos e polígonos.
     

Os jogos com regras são importantes para o desenvolvimento do pensamento lógico, pois a aplicação sistemática das mesmas encaminha a deduções. São mais adequados para o desenvolvimento de habilidades de pensamento do que para o trabalho com algum conteúdo específico. As regras e os procedimentos devem ser apresentados aos jogadores antes da partida e preestabelecer os limites e possibilidades de ação de cada jogador. A responsabilidade de cumprir normas e zelar pelo seu cumprimento encoraja o desenvolvimento da iniciativa, da mente alerta e da confiança em dizer honestamente o que pensa.

Os jogos estão em correspondência direta com o pensamento matemático. Em ambos temos regras, instruções, operações, definições, deduções, desenvolvimento, utilização de normas e novos conhecimentos (resultados).

O trabalho com jogos matemáticos em sala de aula nos traz alguns benefícios:

• conseguimos detectar os alunos que estão com dificuldades reais;
• o aluno demonstra para seus colegas e professores se o assunto foi bem assimilado;
• existe uma competição entre os jogadores e os adversários, pois almejam vencer e par isso aperfeiçoam-se e ultrapassam seus limites;
• durante o desenrolar de um jogo, observamos que o aluno se torna mais crítico, alerta e confiante, expressando o que pensa, elaborando perguntas e tirando conclusões sem necessidade da interferência ou aprovação do professor;
• não existe o medo de errar, pois o erro é considerado um degrau necessário para se chegar a uma resposta correta;
• o aluno se empolga com o clima de uma aula diferente, o que faz com que aprenda sem perceber.

Mas devemos, também, ter alguns cuidados ao escolher os jogos a serem aplicados:

• não tornar o jogo algo obrigatório;
• escolher jogos em que o fator sorte não interfira nas jogadas, permitindo que vença aquele que descobrir as melhores estratégias;
• utilizar atividades que envolvam dois ou mais alunos, para oportunizar a interação social;
• estabelecer regras, que podem ou não ser modificadas no decorrer de uma rodada;
• trabalhar a frustração pela derrota na criança, no sentido de minimizá-la;
• estudar o jogo antes de aplicá-lo (o que só é possível, jogando).  

Temos de formar a consciência de que os sujeitos, ao aprenderem, não o fazem como puros assimiladores de conhecimentos mas sim que, nesse processo, existem determinados componentes internos que não podem deixar de ser ignorados pelos educadores.

Não é necessário ressaltar a grande importância da solução de problemas, pois vivemos em um mundo o qual cada vez mais, exige que as pessoas pensem, questionem e se arrisquem propondo soluções aos vários desafios os quais surgem no trabalho ou na vida cotidiana.

Para a aprendizagem é necessário que o aprendiz tenha um determinado nível de desenvolvimento. As situações de jogo são consideradas parte das atividades pedagógicas, justamente por serem elementos estimuladores do desenvolvimento. É esse raciocínio de que os sujeitos aprendem através dos jogos que nos leva a utilizá-los em sala de aula.

Muitos ouvimos falar e falamos em vincular teoria à prática, mas quase não o fazemos. Utilizar jogos como recurso didático é uma chance que temos de fazê-lo. Eles podem ser usados na classe como um prolongamento da prática habitual da aula. São recursos interessantes e eficientes, que auxiliam os alunos.

A seguir, apresentamos um exemplo de um jogo de adivinhação do número pensado. Essas atividades são problemas aritméticos disfarçados, baseadas no desenvolvimento de expressões matemáticas que levam a uma identidade ou igualdade algébrica a qual verificamos sempre, para qualquer valor da variável que contenha a expressão.

A atividade a seguir reforça o cálculo mental a permite aplicar as propriedades dos números.

 "Adivinhando a idade de uma pessoa''

 

Podemos adivinhar a idade de uma pessoa pedindo-lhe que realize os seguintes cálculos:

1º Escrever um número de dois algarismos.

2º Multiplicar o número escrito por dois.

3º Somar cinco unidades ao produto obtido.

4º Multiplicar esta soma por cinqüenta

5º Somar ao produto o número 1750.

6º Subtrair o ano do nascimento.

O resultado que se obtém é um número de quatro algarismos abcd. Os dois algarismos da direita, que correspondem às dezenas e às unidades, indicam a idade da pessoa e, os dois algarismos da esquerda, que correspondem às centenas e aos milhares, indicam o número que a pessoa havia pensado.

   

A explicação matemática em que essa atividade se baseia é a seguinte:

1º Suponhamos que o número pensado seja ab cuja a expressão polinomial é 10a + b

2º O produto deste número por dois é:

(10a + b) x 2 = 20a + b

3º Somando cinco unidades ao produto, temo:

20a + b + 5

4º Multiplicando a soma anterior por cinqüenta, encontramos:

(20a + 2b + 5) x 50 = 1000a + 100b + 250

5º Acrescentando 1750 ao produto temos (1750 + 250 = 2000).

O acréscimo do número 1750 não se faz por acaso, mas porque 1750 mais 250, que resulta da operação anterior, é igual a 2000, número que indica o ano atual. Devemos tomar cuidado ao acrescentar esse último valor, tomando por base que estamos no ano 2000.

6º Ao resultado anterior, subtrai-se o ano de nascimento da pessoas que está fazendo os cálculos. Se N é o ano de nascimento, então o número obtido será:

1000a + 100b + 2000 - N

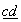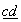Nota-se que, ao subtrair do ano atual o ano do nascimento, obtém-se a idade da pessoa que realiza o jogo. Expressemos por o resultado da operação (2000 - N).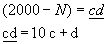

Então, o resultado final é:

1000a + 100b + 10c + d

Esse resultado é a expressão polinomial do número de quatro algarismos abcd, onde os dois algarismos da direita ''cd'', que correspondem às dezenas e unidades, expressam a idade da pessoa que realizou os cálculos, os algarismos da esquerda ''ab'', que correspondem aos milhares a às centenas, nos indicam o número que a pessoa havia pensado.

Vamos ver um exemplo:

1º O número pensado é 57.

2º O produto deste número por dois é: 57 x 2 = 114

3º Somando cinco unidades: 114 + 5 = 119

4º Multiplicando a soma obtida por 50: 119 x 50 = 5950

5º Somando o número 1750 (pois estamos no ano de 2000):

   5950 + 1750 = 7700

6º Subtraindo o ano de nascimento, suponhamos que a pessoa que realizou os cálculos nasceu no ano de 1947, portanto, tem 53 anos ou vai completar 53 anos.

7700 - 1947 = 5753

O resultado final (5753) é um número de quatro algarismos. Os dois algarismos da direita (53) nos indica a idade da pessoa (ou quantos anos ela completará no corrente ano) e os dois algarismos da esquerda (57) nos indicam o número de dois algarismos que a pessoa havia pensado.

É interessante para o professor, nessa atividade de adivinhação de números desenvolver o exercício no quadro de giz de forma coletiva analisando com os alunos as propriedades que aplicou, levando-os a descobrir o ''truque matemático'' utilizado. Também deve pedir aos alunos que criem outros jogos utilizando as propriedades analisadas.

 "O sim"

 

Outra atividade interessante é o jogo chamado ''O sim'', para duas pessoas, usando lápis e papel, (denomina-se assim em honra ao seu inventor, Gustavus I. Simmons).

Necessitamos de lápis de diferentes cores, um para cada jogador e um tabuleiro onde estão marcados os vértices de um polígono.

O objetivo do jogo, para cada participante, consiste em traçar segmentos que unam dois pontos quaisquer do tabuleiro, de tal forma que não se formem triângulos com três lados da mesma cor.

Só contam os triângulos cujos vértices sejam pontos do tabuleiro inicial.

REGRAS DO JOGO

1.  tira-se a sorte para saber que jogador começa a partida.
2. Os jogadores, um de cada vez, traçam um segmento, unindo dois pontos quaisquer da figura.
3. Um jogador utiliza um lápis de uma cor e o outro de cor diferente.
4. Perde o primeiro jogador que formar um triângulo com três lados da cor que utiliza e cujos vértices são três pontos quaisquer do desenho inicial.

Para praticar esse jogo utilizamos tabuleiros com quatro, cinco ou seis pontos. Os tabuleiros mais adequados para jogar ''O sim'' são os de cinco e os de seis pontos. Os tabuleiros com três ou quatro pontos são jogos muito triviais e os com mais de seis pontos são demasiado complicados.

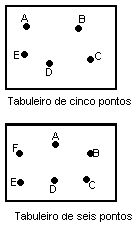
Este jogo introduz um problema interessante e que deve ser proposto aos alunos depois de terem jogado ''O sim'': ''Qual é o número de retas que se podem traçar em um gráfico de n pontos de tal forma que cada uma passe por dois pontos?''

Esse tipo de investigação matemática é muito adequado para desenvolver estratégias de pensamento. A resolução de jogos e problemas possibilita que os alunos encontrem propriedades, relações e regularidades em um conjunto numérico, também, que formulem e comprovem conjecturas sobre uma regra que segue uma série de números.

Para a análise da situação problema completemos a tabela a seguir, com base nas retas desenhadas:

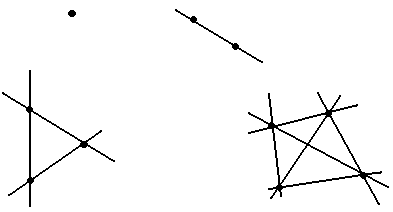
Complete a seguinte tabela:

Número de pontos	1	2	3	4	5	6	7	8	9	10
Número de retas	0	1	3	6	10	15	21	28	36	45

Inicialmente, procuraremos que os alunos obtenham a sucessão de números da segunda fila por via experimental, depois, de forma analítica.

Devemos observar que os números dessa série são os números triangulares, denominados assim, porque cada número é o cardinal de um conjunto de pontos que compõem uma disposição triangular e cuja propriedade mais importante é que, ao somar dois números triangulares consecutivos, obtemos um número quadrado perfeito.

Generalizando, encontramos o número de retas que se podem traçar para n pontos, basta somar ''n'' ao número de diagonais de um polígono de ''n'' vértices ou ''n'' lados.

Chamando de N o número de retas, temos:

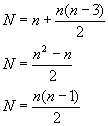
Essa fórmula é similar à que se utiliza para a soma dos ''n'' primeiros números naturais não nulos:

Entre os recursos didáticos citados nos Parâmetros Curriculares Nacionais (PCN) destacam-se os ''jogos''. Segundo os PCN, volume 3, não existe um caminho único e melhor para o ensino da Matemática, no entanto, conhecer diversas possibilidades de trabalho em sala de aula é fundamental para que o professor construa sua prática.

''Finalmente, um aspecto relevante nos jogos é o desafio genuíno que eles provocam no aluno, que gera interesse e prazer. Por isso, é importante que os jogos façam parte da cultura escolar, cabendo ao professor analisar e avaliar a potencialidade educativa dos diferentes jogos e o aspecto curricular que se deseja desenvolver''.

(PCN, 1997,48-49)

Entendemos, portanto, que a aprendizagem deve acontecer de forma interessante e prazerosa e um recurso que possibilita isso são os jogos. Miguel de Guzmán, 1986, expressa muito bem o sentido que essa atividade tem na educação matemática: ''O interesse dos jogos na educação não é apenas divertir, mas sim extrair dessa atividade matérias suficientes para gerar um conhecimento, interessar e fazer com que os estudantes pensem com certa motivação''.

Pesquisa realizada no site:

 http://www.somatematica.com.br/