A Matemática é uma ciência onde se trabalha muito com abstração. Com
a modelagem matemática, podemos aplicar muitos dos conhecimentos de Matemática
adquiridos até o atual estágio do curso, em situações práticas vividas no
dia-a-dia.
A modelagem matemática é um método de investigação que utiliza a
associação das estruturas matemáticas às variáveis e parâmetros de
problemas dos quais necessita-se conhecer soluções com relativa precisão.
Esses procedimentos de investigação da modelagem matemática podem,
também, servir como uma possibilidade metodológica para o ensino de matemática,
porém é necessário ter o cuidado para que isso não seja apenas uma atividade
que procure firmar conceitos matemáticos, mas sim, que leve o aluno a aprender
e a fazer modelos e também adquirir conhecimentos matemáticos.
O tema escolhido para este estudo, foi à construção civil, que está
presente no nosso cotidiano, e demanda de muitos cálculos, quer seja nos
projetos estruturais, arquitetônicos, elétricos e hidráulicos, bem como nas
previsões de quantidades de materiais e seus respectivos custos.
Ao iniciarmos nossa pesquisa, vimos que o assunto é muito amplo e
complexo, por isso decidimos pesquisar alguns aspectos sobre a construção do
telhado, mais especificamente, as tesouras (treliças isostáticas) que servem
para a sustentação da cobertura. Suas barras são dispostas de maneira a
compor uma rede de triângulos, tornando o sistema estrutural indeslocável.
O modelo de tesoura que mais se emprega no Brasil, para estruturas de
madeira dos telhados residenciais é a tesoura inglesa ou howe, conforme vemos
na figura 1. Esse modelo é indicado para casas de até 18,00 metros de vão,
sendo que para casas com largura entre 10 e 18 metros, faz-se necessário
confeccionar as tesouras com peças duplas. Além desta dimensão de vão, a
estrutura passa a ser onerosa e alta, razão pela qual deve-se optar por outros
modelos de estruturas.
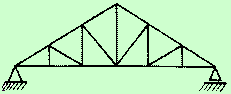
Figura 1 – modelo de tesoura inglesa ou howe
A superfície de
telhado pode ser formada por um ou mais planos (uma água, duas águas, quatro
águas ou múltiplas águas) ou por uma ou mais superfície curvas (arco, cúpula
ou arcos múltiplos).
A cobertura pode ser de telhas cerâmicas, telhas de concreto (planas ou
capa e canal) ou de chapas onduladas de cimento-amianto, aço zincado, madeira
aluminizada, PVC e fiber-glass. As telhas de ardósia e chapas de cobre, foram
praticamente banidas da nossa arquitetura. A figura 2 mostra alguns modelos mais
comuns de telhas cerâmicas.
Figura 2: telhas: francesa, colonial paulista, americana e romana respectivamente.
O ponto do telhado é a relação entre sua altura e a largura ou vão,
que varia entre os limites de 1/2 a 1/8, ou seja, de 100% a 25% de declividade.
De acordo com o tipo de telhas empregado, faz-se necessário adequar o grau de
inclinação do telhado.
As coberturas executadas em chapas onduladas de cimento-amianto,
apresentam vantagem econômica, pois necessitam de menor inclinação do
telhado, além de dispensar o emprego de ripas e caibros, pois apóiam-se
diretamente sobre as terças, permitindo ainda maior distanciamento entre as terças
Os modelos matemáticos deste trabalho foram baseados
em um telhado plano em duas águas, para casas de 6 a 10 metros de largura, com
a utilização de telhas cerâmicas (francesa e colonial paulista) e chapas
onduladas de cimento-amianto, e como já havíamos dito anteriormente, iremos
nos ater apenas aos cálculos relativos às tesouras.
2. Descrição do
Problema
Com os modelos matemáticos que iremos desenvolver a seguir, procuramos
saber qual a quantidade de madeira e o respectivo custo para a construção de
uma tesoura simples, utilizada em casas residenciais, cuja largura varia de 6 a
10 metros.
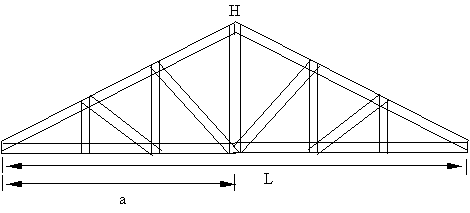
Figura 3 – tesoura howe, com a simbologia utilizada no cálculo de sua altura.
3. Resolução do Problema
Em primeiro lugar, criamos um modelo de cálculo da altura da tesoura (H)
em função da inclinação do telhado (I) e da largura da casa, já acrescida
do beiral (L). Lembramos que a inclinação desejada varia de acordo com o tipo
de telha a utilizar.
altura
largura
(base)
I
1
H a
H a
Aplicando a regra de três:
H . 1 = I . a
H = I . a (1)
H . 1 = I . a
H = I . a (1)
onde:
a = largura dividida por 2, ou seja: L/2
I = inclinação do telhado (em decimais)
H = altura da tesoura
Em seguida, criamos um modelo para cálculo do ângulo de inclinação do telhado ( )
I = inclinação do telhado (em decimais)
H = altura da tesoura
Em seguida, criamos um modelo para cálculo do ângulo de inclinação do telhado ( )
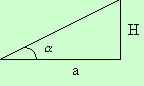
Figura 4 – cálculo do ângulo de inclinação
Aplicando noções de trigonometria, temos:
onde H = I . a
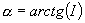
O próximo passo é a criação de um modelo de cálculo do comprimento
do banzo superior (B) da tesoura.
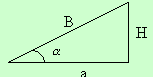
Figura 5 – cálculo do Banzo superior
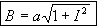(3)onde:
B = comprimento do banzo superior
Feito isso, passamos a calcular o comprimento das verticais e diagonais da tesoura, procedendo da seguinte forma:
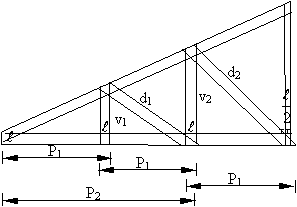
Figura 6 – parte da tesoura, com a simbologia utilizada nos cálculos.
(4)
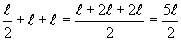
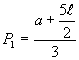
Passamos, agora, ao modelo do cálculo da altura da primeira vertical (v
1),com a utilização de conceitos de trigonometria:
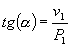
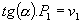
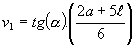(5)
Para que possamos calcular a segunda vertical, procuramos primeiramente, um modelo de cálculo da largura do vão somada à largura da guia (P1 já encontrado), agora, multiplicado por 2 (P1):
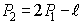
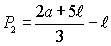
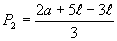
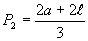
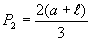(6)Modelo de cálculo da altura da segunda vertical (v2), também aplicando conceitos trigonométricos:
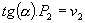
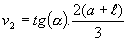(7)
Na seqüência, criamos um modelo de cálculo da primeira diagonal (d1) em relação à altura da primeira vertical (v1) e à largura do vão entre as verticais (P1). Aplicamos, neste caso, novamente o Teorema de Pitágoras
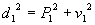
(8)
Necessitamos, ainda, de um modelo de cálculo para a segunda diagonal (d2), em relação à altura da segunda vertical (v2) e à largura do vão entre as verticais (P1), também pelo Teorema de Pitágoras:
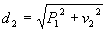(9)
Enfim, para calcular a metragem total de madeira (M) necessária para a
construção de uma tesoura, basta somar a base com a altura, o banzo superior,
as verticais e as diagonais encontradas anteriormente:
M = H + 2(a + B + v1 + v2 + d1 + d2) (10)
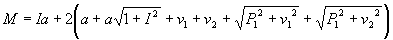
onde:
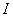= inclinação (em decimais);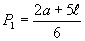
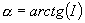
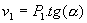
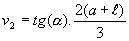
, sendo que L = largura da casa acrescida do beiral.
= largura da guia;
Multiplicando-se a metragem encontrada pelo preço do metro de guia (R),
obteremos o Custo da Madeira de uma tesoura (C).
C = M . R
(11)
Para facilitar na simulação do
modelo matemático, a partir de dados numéricos, permitindo comparativos entre
alguns tipos de telhas empregados nas construções residenciais, e suas
respectivas variações de inclinação, utilizamos o aplicativo MATLAB, e para
isso, criamos um organograma que apresentamos a seguir:
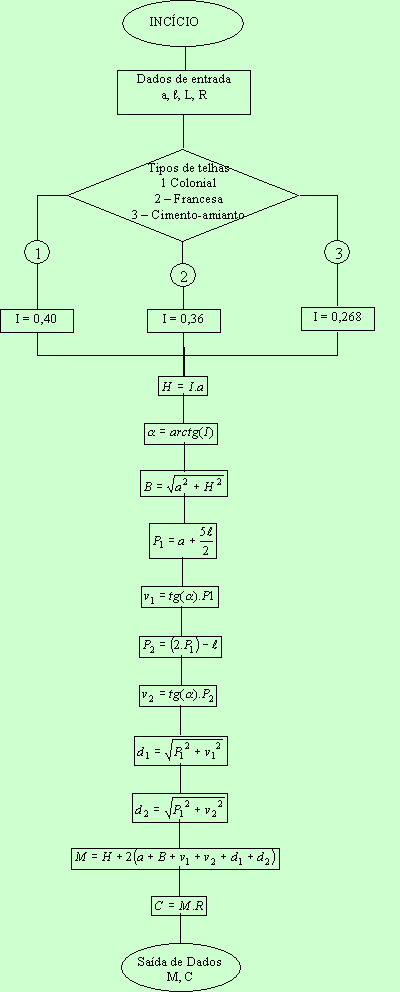
Figura 7 – Organograma para cálculo do modelo no aplicativo MATLAB.
Com o auxílio desse programa, fizemos, então, algumas simulações.
Quanto à inclinação ideal para cada tipo de telha, vimos que existem muitas
discrepâncias, especialmente nos dados fornecidos por fabricantes de telhas.
Optamos em considerar em nossos cálculos, a inclinação mínima sugerida por
Moliterno (1999), e apresentamos, a seguir, alguns dados obtidos.
Tabela 1 – Comparativo dos valores quanto ao tipo de telha
Largura
da Casa
|
6m
|
8m
|
10m
|
|||
Tipo de Telha
|
Metragem
|
Custo
|
Metragem
|
Custo
|
Metragem
|
Custo
|
Colonial
|
21,47
|
69,36
|
28,40
|
91,73
|
35,32
|
114,10
|
Francesa
|
22,87
|
73,86
|
30,24
|
97,67
|
37,61
|
121,49
|
Cimento Amianto
|
19,59
|
63,27
|
25,91
|
83,69
|
32,23
C
|
104,11
|
O gráfico abaixo, nos fornece uma visão de que o tipo de telha e a
conseqüente inclinação do telhado têm influência no custo de fabricação
de uma tesoura, e que as telhas de cimento-amianto apresentam vantagem econômica,
pois necessitam de menor inclinação.
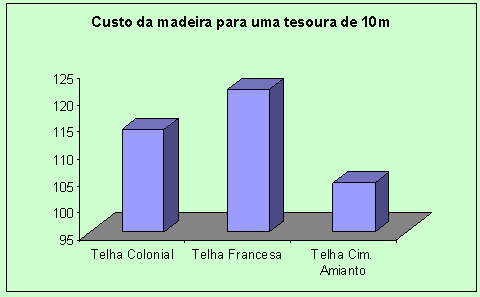
Gráfico 1 –comparativo dos valores quanto ao tipo de telha.
Simulamos, ainda, o comportamento do custo em relação às inclinações
dos telhados, e, conforme gráfico abaixo, vimos que essa variação é
praticamente linear.
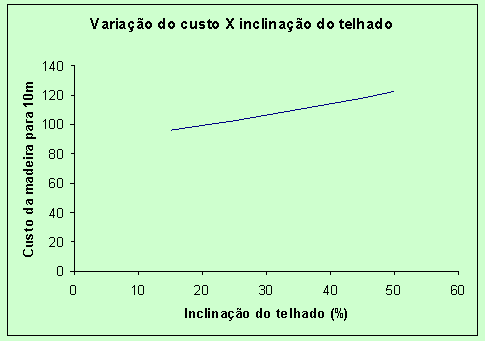
Gráfico 2 – custo de uma tesoura para casa com
10m de largura e sua variação quanto à inclinação do telhado.
Pesquisa realizada no site:
http://www.projetos.unijui.edu.br
Nenhum comentário:
Postar um comentário